Crystal Lattice: -
Regular arrangement of constituent particles in 3-D is called crystal lattice or space lattice.
Unit cell: -
The smallest three dimensional portion of a complete space lattice which when repeated over and again in different direction produces the complete space lattice is called unit cell.
Bravais lattice: -
The fourteen lattices corresponding to seven crystal system are known as Bravais Lattice.
Coordination number: -
Tthe number of spheres touching to a particular sphere.
No. of atoms per unit cell:-
(a) No. of atoms in simple cubic lattice:- 8 atoms are at corner
8*1/8=1
Simple Cubic Latice
8 atoms are at corner and one in the body
8*1/8+1+2
BCC
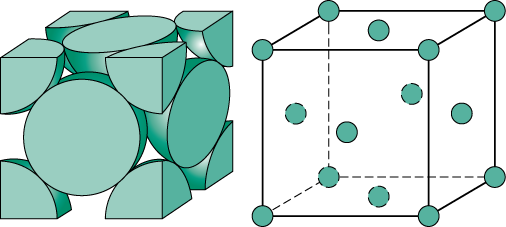
(c) No. of atoms in FCC:-
8 atoms are at corner and six atoms are at faces (one on each face)
8*1/8+6*1/2=4
FCC

Close packing in crystals:-
(a) Close packing in one dimension : - sphere are touching each other in a row. In this arrangement coordination no. is 2
Close packing in one dimension
(b) Close packing in two dimension:- it is done by two ways-
1. Square close packing : - in this arrangement spheres of second row are exactly above the first row.
Square Close Packing
2. Hexagonal close packing: - in this arrangement the spheres of second row may be placed in the depression of the first row.
Hexagonal Close Packing
(c) Close packing in three dimension
1. Three dimensional close packing from two dimensional closed packed layer: - starting from the square close packed layer the second layer and all further layers will be built up such that they are horizontally as well as vertically aligned with each other.
Simple cubic lattice formed by A A A......... arrengment
2. Three dimensional packing from two dimensional hexagonal close packing:- when spheres are arranged in hexagonal close packing in 2-Dthe two types of voids ‘a’& ‘b’ are formed.
‘a’ & ‘b’ voids are triangular when second layer is placed over the void of first layer (only one void is full filled) in hexagonal close packing and these layer form two voids
C – Triangular and D – Octahedral.
A stack of two layers of close packed spheres and voids generated in them. T = Tetrahedral void; O = Octahedral void
Packing efficiency: -
The percentage of the total space filled by the particles is called packing efficiency.
Packing fraction: -
The fraction of the total space filled is called packing fraction.
# Calculation of spaces occupied
1. in a simple cubic unit cell:-
Suppose radius of sphere is = r
Edge length of unit cell = a
As sphere are touching each other
a=2r
No. of sphere per unit cell= 8*1/8=1
Volume of sphere = 4/3πr3
Volume of cube =a3= (2r)3 = 8r3
Packing fraction=
% occupied = 52.4%
2. in face centered cubic structure (Cubic close packing):- spheres of the face center touching the sphere of the corner,
Then, AC = 4r
in ∆ ABC
% occupied = 74%
3. In body centred cubic structure: - Sphere at the body centred touching the sphere of the corner.
Body diagonal, AD = 4r
Further, face diagonal,
% occupied = 68%
=> Radius (r) of the octahedral void =0.414R
=> Radius (r) of the tetrahedral void = 0.225R
In CCP or HCC. If there are N spheres in the packing.
No. of octahedral voids = N
No. of Tetrahedral voids = 2N
Imperfection and defects in solids










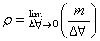


0 Comments