What is the electromagnetic field? Electromagnetic fields are caused by electric charges at rest and in motion. Positive and negative electric charges are sources of the electric fields and moving electric charges yielding a current is the source of magnetic fields. Time-varying electric and magnetic fields are coupled in an electromagnetic field radiating from the source.

Electromagnetic fields are divided into four different quantities:
- the magnetic flux density B with the unit T (Tesla or volt-second per square meter)
- the magnetic field intensity H with the unit A/m (Ampere per meter)
- the electric field intensity E with the unit V/m (Volt per meter)
- the electric flux density D with the unit C/m2 (Coulomb per square meter)
A time-varying E and D will give rise to B and H, and vice versa where the relation depends on the properties of the medium. Far enough from the source the magnetic field, H, will be perpendicular to the electric field, E, and both are normal to the direction of propagation, as shown in the following figure:

Figure 2- A time-varying electric field, E, will give rise to a perpendicular magnetic field, H, and vice versa. Far enough from the source, it will become a uniform plane wave and the ratio between E and H will be the intrinsic impedance of the medium.
The permittivity is a proportionality constant between the electric flux density D and the electric field intensity E, in free space as:
and the permeability is the proportionality constant between the magnetic flux density B and the magnetic field intensity H, in free space as:
From these constants, the intrinsic impedance of free space can be calculated as [8]:
 [W ] [W ] |
Maxwell equations
Maxwell equation in differential form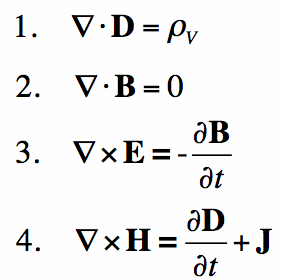
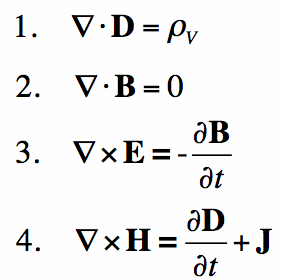
Maxwell equation in integral form

Maxwell’s first equation or Gauss’s law in electrostatics
Statement. It states that the total electric flux φE passing through a closed hypothetical surface is equal to 1/ε0 times the net charge enclosed by the surface:
ΦE=∫E.dS=q/ε0
∫D.dS=q
where D=ε0E= Displacement Vector
Let the charge be distributed over a volume V and p be the volume charge density. therefore
q=∫ pdV
Therefore
∫ D.dS=∫vpdV (1)
(this is the integral form of Maxwell’s first equation or Gauss’s law in electrostatics.)
Differential form:
Apply Gauss’s Divergence theorem to change L.H.S. of equation(1) from surface integral into a volume integral
i.e. ∫ D.dS=∫( ∇.D)dV
Substituting this equation in equation (1), we get
∫ (∇.D)dV=∫v pdV
As two volume integrals are equal only if their integrands are equal
Thus, ∇.D=p (2)
Equation (2) is the Differential form of Maxwell’s first equation.
Maxwell’s second equation or Gauss’s law for Magnetism
Statement.magnetic monopole does not exist i.e. the total magnetic flux φm emerging through a closed surface is zero.
φm=∫B.dS=0 (1)
The equation (1) is the Integral form of Maxwell’s second equation.
This equation also proves that magnetic monopole does not exist.
Differential Form:
Apply Gauss’s Divergence theorem to equation (1)
i.e. ∫s B.dS=∫v(∇.B)dV
As ∫B.dS=0
Thus , ∇ .B=0 (2)
The equation (4) is the differential form of Maxwell’s second equation.
Maxwell third law
Statement. (a) It states that whenever magnetic flux linked with a circuit changes then induced electromotive force (emf) is set up in the circuit. This induced emf lasts so long as the change in magnetic flux continues.
(b) The magnitude of induced emf is equal to the rate of change of magnetic flux linked with the circuit.
Therefore induced emf= – dφm/dt (1)
Where φm=∫B.dS (2)
Here negative sign is because of Lenz’s law which states that the induced emf set up a current in such a direction that the magnetic effect produced by it opposes the cause producing it.
Also, the definition of emf states that emf is the closed line integral of the non-conservative electric field generated by the battery.
That is emf=∫E.dL (3)
Comparing equations (5) and (6), we get
∫E.dL= – ∫s d/d t B.dS (4)
(this is the integral form of Maxwell’s third Equation or Faraday’s law of electromagnetic induction.)
Differential form :
Apply Stoke’s theorem to L.H.S. of equations (4) to change line integral to surface integral.
That is ∫ E.dL=∫( ∇ x E).dS
By substituting above equation in equation(7), we get
∫s ( ∇ x E).dS = -∫ d/d t(B.dS)
As two surface integral are equal only when their integrands are equal.
Thus ∇ x E= – dB/ dt (5)
Equation (5) is the Differential form of Maxwell’s third equation.
pointing theorem and pointing vector
Poynting vector, a quantity describing the magnitude and direction of the flow of energy in electromagnetic waves. It is named after English physicist John Henry Poynting, who introduced it in 1884.
Statement. This theorem states that the cross product of electric field vector, E and magnetic field vector, H at any point is a measure of the rate of flow of electromagnetic energy per unit area at that point, that is
P = E x H
Here P → Poynting vector and it is named after its discoverer, J.H. Poynting. The direction of P is perpendicular to E and H and in the direction of vector E x H
Proof. Consider Maxwell’s fourth equation (Modified Ampere’s Circuital Law), that is
del x H = J + ε dE/dt
or J = (del x H) – ε dE/dt
The above equation has the dimensions of current density. Now, to convert the dimensions into the rate of energy flow per unit volume, take the dot product of both sides of the above equation by E, that is
E. J = E. (del x H) – εE. dE/dt (1)
Use vector Indentity
del. (E x H) = H. (del x E) – E. (del x H)
or E. (del x H) = H. (del x E) – del ( E x H )
By substituting value of E. (del x H) in equation (1) , we get
E. J. =H. (del x E) – del. (E x H) – εE dE/dt (2)
also from Maxwell’s third equation (Faraday’s law of electromagnetic induction).
del x E = μdH/dt
By substituting value of del x E in equation (2) we get
E. J. =μH . (dH)/dt – εE. dE/dt – del . (E x H) (3)
We can write
H. dH/dt = 1/2 dH2/dt (4a)
E. dE/dt = 1/2 dE2/dt (4b)
By substituting equations 4a and 4b in equation 3, we get
E. J. = -μ/2 dH 2/dt – ε/2 dE 2/dt – del . (E x H)
E. J. = -d/dt [ dH 2/2 + εE2 /2] – del . (E x H)
By taking volume integral on both sides, we get
∫E. J. dV = -d/dt ∫ [μ H 2 /2 + εE2/2 ] dV – ∫del . (E x H) dV (5)
apply Gauss’s Divergence theorem to second term of R.H.S., to change volume integral into surface integral, that is
∫del . (E x H) dV = ∫ (E x H) . dS
Substitute above equation in equation 5
Thus
∫E. J. dV = -d/dt ∫[ ε E2/2 + μ H2/2] dV – ∫(E x H) . dS (6)
or ∫ (E x H) . dS = ∫-d/dt [ ε E 2 /2 + μ H 2 /2] dV –∫ E. J. dV
Interpretation of above equation :
L.H.S. Term
∫ (E x H) . dS → It represents the rate of outward flow of energy from a volume S
V and the integral is over the closed surface surrounding the volume. This rate of outward flow of power from a volume V is represented by
∫ P . dS = ∫ (E x H) . dS
where Poynting vector, P = E x H
Inward flow of power is represented by
– ∫ P . dS = – φ∫ (E x H) . ds
R.H.S. First Term
-d /dt [μ H 2/2 + ε E 2 /2] dV → If the energy is flowing out of the region, there must be a corresponding decrease of electromagnetic energy. So here negative sign indicates decrease. Electromagnetic energy is the sum of magnetic energy, μ H 2/2 and electric
energy, ε E 2/2 . So first term of R.H.S. represents rate of decrease of stored electromagnetic 2 energy.
R.H.S. Second Term
∫ (E. J) dV →Total ohmic power dissipated within the volume.
So from the law of conservation of energy, equation (6) can be written in words as-
The Rate of energy disripation in volume V = Rate at which stored electromagnetic energy is decreasing in V + Inward rate of flow of energy through the surface of the volume.
The Rate of energy disripation in volume V = Rate at which stored electromagnetic energy is decreasing in V + Inward rate of flow of energy through the surface of the volume.
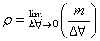


0 Comments